NÉGOCIATIONS TARIFAIRES DANS LE DOMAINE DE
L'AGRICULTURE
Méthodes de réduction
Comprendre le sens des réductions “à pourcentage fixe” et des réductions selon la formule “d'harmonisation”, de l'approche du “Cycle d'Uruguay” et des formules suissesDifférentes méthodes sont possibles en matière de réductions tarifaires négociées. Certaines sont plus courantes que d'autres. Certaines reposent sur des formules. Même une fois convenue une méthode ou une combinaison de méthodes, le résultat final pour tel ou tel produit peut dépendre de négociations entre pays sur les taux de tarifs appliqués aux produits en question.
> Historique
des négociations sur l'agriculture
Ce document d'information a
été établi par la Division de l'information et des relations avec les
médias du Secrétariat de l'OMC pour aider le public à mieux comprendre
les négociations sur l'agriculture. Il ne constitue pas une
interprétation officielle des accords de l'OMC ni des positions des
Membres.
Taux unique: Les tarifs sont ramenés à un taux unique pour tous
les produits. Théoriquement, c'est le résultat le plus simple. En
pratique, cette méthode est principalement utilisée pour les accords
régionaux de libre-échange dans le cadre desquels le taux de tarif final
est égal à zéro, ou est peu élevé, pour les échanges à l'intérieur du
groupe.
Réduction sur la base d'un pourcentage uniforme: Le même
pourcentage de réduction pour tous les produits, que le tarif de départ
soit élevé ou bas. Par exemple, tous les tarifs seraient réduits de 25
pour cent par étapes égales sur une période de cinq ans.
Approche du Cycle d'Uruguay: Les négociations du Cycle d'Uruguay
(1986-1994) dans le domaine de l'agriculture ont abouti à un accord
prévoyant que les pays développés réduiraient les tarifs sur les
produits agricoles d'une moyenne de 36 pour cent sur six ans (6 pour
cent par an) avec un minimum de 15 pour cent pour chaque produit pendant
la période considérée.
Réductions selon la formule d'harmonisation: Il s'agit
principalement d'effectuer des réductions plus importantes pour les
tarifs élevés et de combler l'écart entre les tarifs finals
(“harmoniser” les taux):
- Différents pourcentages pour différentes fourchettes de tarifs. Par exemple, pas de réduction pour les tarifs compris entre 0 et 10 pour cent, réductions de 25 pour cent pour les tarifs compris entre 11 et 50 pour cent, réductions de 50 pour cent pour les tarifs supérieurs, etc. Une variante pourrait consister à supprimer tous les tarifs inférieurs à 5 pour cent qui sont parfois considérés comme des tarifs de nuisance présentant peu d'avantages. Il pourrait s'agir de réductions simples ou moyennes à l'intérieur de chaque fourchette.
- Des formules mathématiques conçues pour réduire plus fortement (c'est à dire opérer des réductions en pourcentages plus importantes) les tarifs élevés. La “formule suisse” en est un exemple (plus de détails ci après).
Autres méthodes: Il existe un certain nombre de possibilités:
- Taux différents pour différentes catégories de produits. Par exemple, des réductions plus importantes pour les produits transformés que pour les matières premières. Il s'agit d'essayer de pallier la “progressivité des tarifs” par laquelle les pays protègent leurs industries de transformation en pratiquant des prix bas sur les matières premières importées et des prix élevés sur les produits transformés importés.
-
Combinaisons de l'une ou l'autre de ces
méthodes.
L'“APPROCHE DU CYCLE D'URUGUAY” > haut
de page
Exemple reposant sur des réductions moyennes de 36 pour cent sur une période de six ans (6 pour cent par an)
Négocier une réduction tarifaire sur la base d'un pourcentage moyen
donné sur un certain nombre d'années avec la possibilité d'une
réduction minimale plus faible pour certains produits elle
a été l'approche finalement adoptée dans le cadre des négociations
sur l'agriculture du Cycle d'Uruguay (1986-1994).
Cette approche comporte deux caractéristiques:
- les réductions sur la base d'un pourcentage uniforme entraînent des abaissements plus faibles pour les tarifs élevés et un éventail de tarifs finals plus large qu'une méthode d'harmonisation comme la formule suisse (voir le tableau);
- la combinaison de chiffres de réduction moyens et minimaux donne aux pays une certaine flexibilité, c'est-à-dire qu'ils peuvent varier les réductions tarifaires effectives pour certains produits (c'est ce que l'on désigne sous le terme technique de “lignes tarifaires”) — même si la réduction moyenne est de 36 pour cent, certaines réductions seront plus importantes, d'autres moins, et il est possible qu'aucun tarif ne soit en fait réduit de ce pourcentage précis.
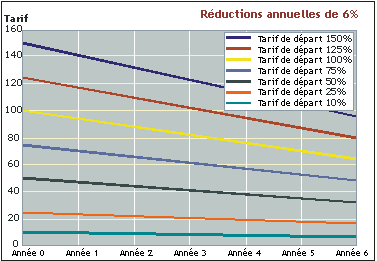
Le tableau ci-dessous montre que, lorsque les tarifs de départ sont
élevés, les taux finals restent assez élevés: une réduction de 36
pour cent à partir d'un taux de 150 pour cent donne un taux final de
96 pour cent la sixième année. C'est seulement lorsque les tarifs de
départ sont bas que les tarifs finals atteignent des taux proches de
la formule suisse (comme dans l'exemple): si les tarifs de départ
sont de 10 pour cent et 25 pour cent, les taux obtenus la sixième
année sont de 6,4 pour cent et de 16 pour cent. L'éventail des
tarifs finals, qui va de 6,4 pour cent à 96 pour cent, reste large.
Le chiffre de 36 pour cent a été utilisé durant le Cycle d'Uruguay,
même si d'autres chiffres auraient pu être utilisés dans le cadre de
l'approche du Cycle d'Uruguay. Cependant, il s'agissait de
réductions tarifaires moyennes — 36 pour cent sur une période
de six ans, pour les pays développés, avec un objectif moyen
distinct de 24 pour cent sur une période de dix ans pour les pays en
développement.
|
|
Tarif de départ 150% |
Tarif de départ 125% |
Tarif de départ 100% |
Tarif de départ 75% |
Tarif de départ 50% |
Tarif de départ 25% |
Tarif de départ 10% |
| Réduction (%) | 36 | 36 | 36 | 36 | 36 | 36 | 36 |
| Année 0 | 150,00 | 125,00 | 100,00 | 75,00 | 50,00 | 25,00 | 10,00 |
| Année 1 | 141,00 | 117,50 | 94,00 | 70,50 | 47,00 | 23,50 | 9,40 |
| Année 2 | 132,00 | 110,00 | 88,00 | 66,00 | 44,00 | 22,00 | 8,80 |
| Année 3 | 123,00 | 102,50 | 82,00 | 61,50 | 41,00 | 20,50 | 8,20 |
| Année 4 | 114,00 | 95,00 | 76,00 | 57,00 | 38,00 | 19,00 | 7,60 |
| Année 5 | 105,00 | 87,50 | 70,00 | 52,50 | 35,00 | 17,50 | 7,00 |
| Année 6 | 96,00 | 80,00 | 64,00 | 48,00 | 32,00 | 16,00 | 6,40 |
| Étapes annuelles (points de pourcentage) | 10,80 | 9,00 | 7,20 | 5,40 | 3,60 | 1,80 | 0,72 |
| Comparaison: Formule suisse, année 6, avec un coefficient=25 | 21,43 | 20,83 | 20,00 | 18,75 | 16,67 | 12,50 | 7,14 |
LA FORMULE SUISSE
UN TYPE PARTICULIER DE RÉDUCTION TARIFAIRE SELON UNE
FORMULE D'HARMONISATION
> haut
de page
Négocier un écart beaucoup plus étroit entre les tarifs élevés et les tarifs bas avec un tarif maximal intégré Par harmonisation des tarifs, il faut entendre réduction importante de l'écart entre les tarifs élevés et les tarifs bas. La “formule suisse” est un type particulier de méthode d'harmonisation. Elle utilise une formule mathématique unique pour donner:
- un éventail étroit de taux de tarifs finals à partir d'un large éventail de tarifs initiaux;
- un taux final maximal, aussi élevé qu'ait été le tarif initial.
Normalement, les réductions prescrites sont alors échelonnées en
étapes annuelles égales.
La formule a été proposée par la Suisse durant les négociations du
Tokyo Round (1973-1979) mais la Suisse est opposée à l'utilisation
de cette méthode pour les négociations en cours sur l'agriculture;
elle préfère l'approche du Cycle d'Uruguay alors que l'Uruguay
préfère la formule suisse!
Un élément essentiel est un chiffre, qui est négocié et intégré dans
la formule. On l'appelle “coefficient” (“A” dans la formule
ci-dessous). Cela détermine également le taux de tarif final maximal.
Laformule
|
Z = AX/(A+X) |
où
X = taux de tarif initial
A = coefficient et taux de tarif final maximal
Z = taux de tarif inférieur résultant (à la fin de la période)
tiré de Goode: Dictionary of Trade Policy Terms, Centre for International Economic Studies, University of Adelaide
> Voir également “mathématiquement parlant”
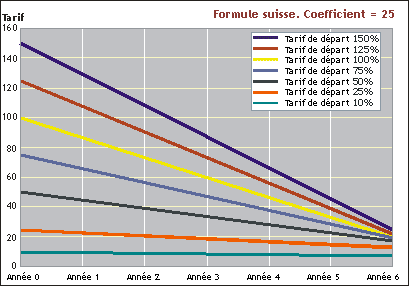
haut de pageExemple
Comment une formule suisse avec un coefficient de 25 fonctionne sur
une période de six ans
Le coefficient de 25 définit également le tarif maximal à la fin de
la période.
|
Tarif de départ 150% |
Tarif de départ 125% |
Tarif de départ 100% |
Tarif de départ 75% |
Tarif de départ 50% |
Tarif de départ 25% |
Tarif de départ 10% |
|
| Coefficient | 25 | 25 | 25 | 25 | 25 | 25 | 25 |
| Année 0 | 150,00 | 125,00 | 100,00 | 75,00 | 50,00 | 25,00 | 10,00 |
| Année 1 | 128,57 | 107,64 | 86,67 | 65,63 | 44,44 | 22,92 | 9,52 |
| Année 2 | 107,14 | 90,28 | 73,33 | 56,25 | 38,89 | 20,83 | 9,05 |
| Année 3 | 85,71 | 72,92 | 60,00 | 46,88 | 33,33 | 18,75 | 8,57 |
| Année 4 | 64,29 | 55,56 | 46,67 | 37,50 | 27,78 | 16,67 | 8,10 |
| Année 5 | 42,86 | 38,19 | 33,33 | 28,13 | 22,22 | 14,58 | 7,62 |
| Année 6 | 21,43 | 20,83 | 20,00 | 18,75 | 16,67 | 12,50 | 7,14 |
| Étapes annuelles (points de pourcentage) | 21,43 | 17,36 | 13,33 | 9,38 | 5,56 | 2,08 | 0,48 |
| Réduction (en %) sur six ans | 85,71 | 83,33 | 80,00 | 75,00 | 66,67 | 50,00 | 28,57 |
| Comparaison: Année 6 pour une réduction sur la base d'un taux uniforme de 36 pour cent | 96,00 | 80,00 | 64, 00 | 48,00 | 32,00 | 16,00 | 6,40 |
Mathématiquement parlant … > haut
de page
Comment le coefficient de la formule suisse définit le tarif final maximal:
En partant de la formule Z=AX/(A+X),
au fur et à mesure que le tarif initial X tend vers l'infini,
X/(A+X) s'approche de 1,
ce qui donne Z=Ax1.
Pour en savoir plus sur les formules de réduction des tarifs:
Il existe beaucoup d'autres approches en matière de formules de réduction des tarifs. Voir le document de l'OMC TN/MA/S/3/Rev.2 intitulé “Approches des négociations tarifaires fondées sur une formule” (révision), du 11 avril 2003, établi par le Secrétariat pour les négociations sur l'accès aux marchés pour les produits non agricoles.
